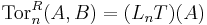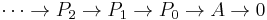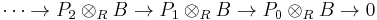Tor functor

In homological algebra, the Tor functors are the derived functors of the tensor product functor. They were first defined in generality to express the Künneth theorem and universal coefficient theorem in algebraic topology.

Specifically, suppose R is a ring, and denote by R-Mod the category of left R-modules and by Mod-R the category of right R-modules (if R is commutative, the two categories coincide). Pick a fixed module B in R-Mod. For A in Mod-R, set T(A) = A⊗_RB. Then T is a right exact functor from Mod-R to the category of abelian groups Ab (in the case when R is commutative, it is a right exact functor from Mod-R to Mod-R) and its left derived functors L_nT are defined. We set

$\mathrm{Tor}_n^R(A,B)=(L_nT)(A)$

i.e., we take a projective resolution

$\cdots\rightarrow P_2 \rightarrow P_1 \rightarrow P_0 \rightarrow A\rightarrow 0$

then tensor the projective resolution with B to get the complex

$\cdots \rightarrow P_2\otimes_R B \rightarrow P_1\otimes_R B \rightarrow P_0\otimes_R B \rightarrow 0$

(note that 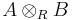$A\otimes_R B$ does not appear and the last arrow is just the zero map) and take the homology of this complex.

Properties

For every n ≥ 1, Tor_n^R is an additive functor from Mod-R × R-Mod to Ab. In the case when R is commutative, we have additive functors from Mod-R × Mod-R to Mod-R.

As is true for every family of derived functors, every short exact sequence

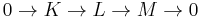
$0\rightarrow K\rightarrow L\rightarrow M\rightarrow 0$

induces a long exact sequence of the form

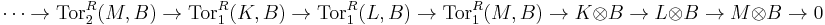$\cdots\rightarrow\mathrm{Tor}_2^R(M,B)\rightarrow\mathrm{Tor}_1^R(K,B)\rightarrow\mathrm{Tor}_1^R(L,B)\rightarrow\mathrm{Tor}_1^R(M,B)\rightarrow K\otimes B\rightarrow L\otimes B\rightarrow M\otimes B\rightarrow 0$ .

If R is commutative and r in R is not a zero divisor then

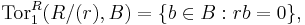
$\mathrm{Tor}_1^R(R/(r),B)=\{b\in B:rb=0\},$

from which the terminology Tor (that is, Torsion) comes: see torsion subgroup.

In the case of abelian groups (i.e. if R is the ring of integers Z), then Tor_n^Z(A,B) = 0 for all n ≥ 2. The reason: every abelian group A has a free resolution of length 1, since subgroups of free abelian groups are free abelian. So in this important special case, the higher Tor functors are invisible. In addition, Tor₁^Z(Z_k,A) = Ker(f) where f represents "multiplication by k".

Furthermore, every free module has a free resolution of length zero, so by the argument above, if F is a free R-module, then Tor_n^R(F,B) = 0 for all n ≥ 1.

The Tor functors commute with arbitrary direct sums: there is a natural isomorphism

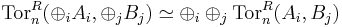$\mathrm{Tor}_n^R(\oplus_i A_i, \oplus_j B_j) \simeq \oplus_i \oplus_j \mathrm{Tor}_n^R(A_i,B_j)$ . Indeed, the Tor functors even preserve arbitrary colimits.

From the classification of finitely generated abelian groups, we know that every finitely generated abelian group is the direct sum of copies of Z and Z_k. This together with the previous three points allows us to compute Tor₁^Z(A, B) whenever A is finitely generated.

A module M in Mod-R is flat if and only if Tor₁^R(M, -) = 0. In this case, we even have Tor_n^R(M, -) = 0 for all n ≥ 1 . In fact, to compute Tor_n^R(A, B), one may use a flat resolution of A or B, instead of a projective resolution (note that a projective resolution is automatically a flat resolution, but the converse isn't true, so allowing flat resolutions is more flexible).

References

Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, ISBN 978-0-521-55987-4, OCLC 36131259, MR 1269324

Tor functor

Properties

See also

References